
In questo nuovo articolo ti spiegherò cosa sono i numeri primi e come riconoscerli. Fatto questo ti metterò a disposizione una tabella per una loro rapida consultazione ed un file excel per la loro creazione.
Cosa sono i numeri primi
Innanzitutto per capire cosa sono i numeri primi dobbiamo affermare che essi fanno parte di quella parte della matematica che studia i numeri interi.
Quindi i numeri primi, a differenza dei numeri composti, sono tutti quei numeri che possono essere divisi solo per 1 e per se stessi dando ovviamente come risultato un numero intero.
Facciamo alcuni esempi pratici di numeri primi e numeri composti:
- 2 = (2, 1) – In pratica il numero 2 è divisibile come detto precedentemente per se stesso (ovvero 2) e per 1 e quindi è un numero primo;
- 3 = (3, 1) – il numero 3 è divisibile solo per 3 e per 1 e quindi è un numero primo;
- 4 = (4, 2, 1) – il numero 4 è divisibile invece per 4, per 2 e per 1 e di conseguenza non soddisfa i criteri precedentemente menzionati e quindi è un numero composto;
- 6 = (6, 3, 2, 1) – il numero 6 è divisibile invece per 6, per 3, per 2 e per 1 e di conseguenza non soddisfa i criteri precedentemente menzionati e quindi è un numero composto.
Altri numeri primi sono il 5, 7, 11, 13, 17 ecc.
Ricapitolando, per essere numeri primi devono essere soddisfatte queste 4 proprietà:
- essere la base di tutti gli altri numeri;
- non essere multipli;
- non essere 1 o 0;
- avere solo ed esclusivamente due divisori, il numero 1 e se stessi.
Perché 1 non fa parte dei numeri primi?
A differenza di molte credenze popolari, il numero 1 non appartiene alla categoria dei numeri primi.
Questo perché se si ammettesse che lo fosse si violerebbe il Teorema Fondamentale dell’Aritmetica che recita quanto segue:
Ogni numero naturale maggiore di 1 o è un numero primo oppure è un numero esprimibile in una maniera unica come prodotto di numeri primi.
2, 5, 13 sono numeri primi, e come tale possono essere espressi soltanto come loro stessi.
6 è un numero non primo, e infatti può essere espresso come 2 x 3.
E 1? Qual’è il problema col numero 1?
Il problema risiede che un qualsiasi numero X moltiplicato per 1 da sempre per risultato X: X∗1=X
Riprendiamo di nuovo al caso del numero 6. Cosa accadrebbe se ammettessimo che 1 è un numero primo? Accadrebbe che esisterebbero infinite maniere per esprimere 6 come prodotto di numeri primi!
2∗3=6 oppure 2∗3∗1=6 o ancora 2∗3∗1∗1=6
Puoi aggiungere infiniti 1 al prodotto originario. Ma questo viola il teorema prima presentato.
Di conseguenza 1 non può essere un numero primo.
Non è neppure un numero composto, poiché non esistono un prodotto di due numeri interi che dia come risultato 1. Esso è, come lo 0, fa categoria a sé stante.
Come riconoscere i numeri primi
Purtroppo non è sempre semplice riconoscere i numeri primi sopratutto quando questi hanno un valore molto elevato, ma per fortuna in questo caso ci viene in aiuto il criterio di divisibilità che ci permette di stabilire velocemente se un numero è primo oppure no.
Elenchiamo alcuni esempi di criteri di divisibilità che ci fanno subito capire se il numero in questione è un numero primo oppure no:
- tutti i numeri pari, eccetto 2, non sono numeri primi;
- Tutti i numeri che terminano con 5, eccetto proprio il 5, non sono numeri primi proprio perchè sono tutti divisibili per 5
- tutti i numeri, eccetto 3, la cui somma delle cifre è un multiplo di 3
Quanti sono i numeri primi?
I numeri primi non hanno un valore definito poiché sono infiniti e per questo motivo non è possibile elencarli tutti.
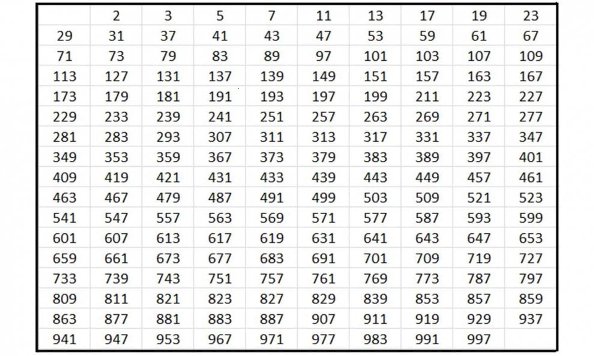
Tabella numeri primi
Di seguito trovi una tabella in cui trovi tutti numeri primi da 1 a 1000
Se avete portato a termine la lettura avrete ora capito cosa sono i numeri primi e come riconoscerli. Se avete bisogno di elaborare numeri primi superiori a quelli elencati nella tabella precedente potrete scaricare questo file Excel:
Scarica questo file: Generatore di numeri primi

